Algorithmes et Programmation 2, année 2022
TD 2
L’objectif de ce TP est d’approfondir la récursivité et les calculs de complexité simple pour certaines fonctions.
Rappel Rendre le TP
Le TD doit être rendu sur Moodle avant le début du TD suivant. En cas de TD non rendu, vous aurez automatiquement 0, sauf cas exceptionnel.
Le rendu doit être un dossier compressé au format zip contenant:
- Un fichier contenant les réponses
- Un fichier par exercice du TD
Chaque fonction présente dans le TD doit contenir une documentation et un nom clair.
Les TP peuvent être rendus en binômes et le nom du binôme doit apparaître clairement dans le fichier réponses. Si une réponse est faite à plus que deux, vous devez l’indiquer dans le fichier réponse. Si ce n’est pas indiqué, cela sera considéré comme du plagiat.
Si vous utilisez du code sur internet, vous devez indiquer la source dans le code source et dans le fichier réponse. Si ce n’est pas indiqué, cela sera considéré comme du plagiat.
Des scripts automatiques sont exécutés pour vérifier cela pour chaque rendu, ne tentez pas la chance …
Exercice 1
Un étudiant de L2 MIASHS un rendu un TD en oubliant de respecter les consignes! Il a très mal nommé ses fonctions et ne leur à pas mis de documentations.
Afin qu’il n’ait pas 0, renommez les fonctions et écrivez pour lui la documentation.
Exercice 2
La suite de Fibonacci \((f_n)\) est définie par récurrence
\[ \begin{cases} f_0 = f_1 = 1 \\ f_{n+2} = f_{n+1} + f_n \end{cases} \]
Écrire une fonction
fibonaccirécursive qui prend en argument un entier \(n\) et retourne \(f_n\), le \(n\)ème terme de la suite de Fibonacci.Analyser la complexité de la fonction.
Écrire une fonction récursive de complexité linéaire qui prend en argument un entier \(n\) et retourne le couple \((f_n, f_{n-1})\). En déduire une fonction
fibonacci2qui prend en argument un entier \(n\) et retourne \(f_n\).(Difficile) Mémoisation
Écrire un décorateur (une fonction de fonction, voir ici) qui prend en argument:
- Une fonction \(f\) qui prend en argument un entier
- Un dictionnaire \(D\)
et qui retourne une nouvelle fonction \(nf\) qui prend en argument un entier et:
- si cet entier est une clef de \(D\) retourne la valeur associé
- sinon exécute la fonction \(f\) et stocke le résultat dans \(D\) et le retourne.
Décorez la fonction fibonacci de la première question.
Quelle la complexité de la fonction décorée? Quelle est la complexité en
espace?
Exercice 3:
Voici la spécification du problème decoupe
- decoupe
- Entrée: une chaîne de caractère \(u\) et un charactère \(s\)
- Retourne: une liste de chaînes \(u_1,\ldots,u_n\) tel que \(u=u_1\cdot s \cdot u_2\cdot s \cdots s\cdot u_n\)
Par exemple, decoupe("aabacbddddbebf","b") retourne la
liste ["aa", "ac", "dddd", "e", "f"].
Écrire une version itérative de la fonction
decoupeÉcrire une version récursive de la fonction
decoupeFaire l’analyse de complexité de chaque implémentation
Exercice 4: Les ensembles de Mandelbrot
Pour \(c\in\mathbb{C}\), on définit la suite complexe
\[ \begin{cases} z_0 = 0\\ z_{n+1} = z_n^2 + c \end{cases} \]
Cette suite peut converger ou diverger en fonction de la valeur de \(c\). On sait qu’elle diverge quand son module est supérieur à 2.
- Écrire une fonction récursive
mandelbrotqui prend en argument le nombre complexe \(c\) et \(n\) et retourne \(z_n\) ou \(2\) si le module de \(z_n\) est supérieur à \(2\). Écrire une fonctionmandelbrot_modulequi prends en argument un nombre complexe \(c\) et un entier \(n\) et retourne le module de \(z_n\) si celui ci est plus petit que \(2\) et \(2\) sinon.
Les complexes sont gérés nativement par Python sans effort. Le nombre
\(13+4i\) s’écrit
13 + 4j.
- Écrire une fonction
fenetrequi prend en argument un nombre complexe \(O\) (l’origine), un float \(D\) (le diametre), et un entier \(n\) (nombre de points) et retourne la liste de liste \(L\) tel que pour tout \(a,b< n\) on a \(L[a][b] = O + (a*\frac{D}{n} - \frac{D}{2}) + (b*\frac{D}{n} - \frac{D}{2})j\)
Vous pouvez le faire à la main facilement ou utiliser la
fonction arange du module Python numpy
On peut voir une liste contenant \(n\) liste de taille \(m\) comme une matrice \(n\times m\).
À l’aide d’une ou plusieurs application de
map, construisez une fonction qui prends une liste de liste de complexe et applique la fonction Mandelbrot sur chaque point.Pour dessiner une matrice en Python, on peut utiliser le module
matplotlibetnumpycomme suit:
import matplotlib.pyplot as plt
import numpy as np
L = [
[0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 0, 1, 0, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 1, 0, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]
]
M = np.array(L) # Tranforme la liste de liste en tableau numpy
plt.imshow(M)
plt.axis("off") # enlève les axes, inutile ici
plt.show() # dessine le resultat
Les couleurs peuvent être changées (voir ici)
Dessiner les ensembles de Mandelbrot:
- centrés en \(0\), de diamètre 3 avec un nombre d’itération de 20

- centrés en
-0.06783611264225832 + 0.6617460391250546jde diamètre0.001, en faisant varier l’itération entre 33 et 160, on obtient les images suivantes (assemblées en un gif):
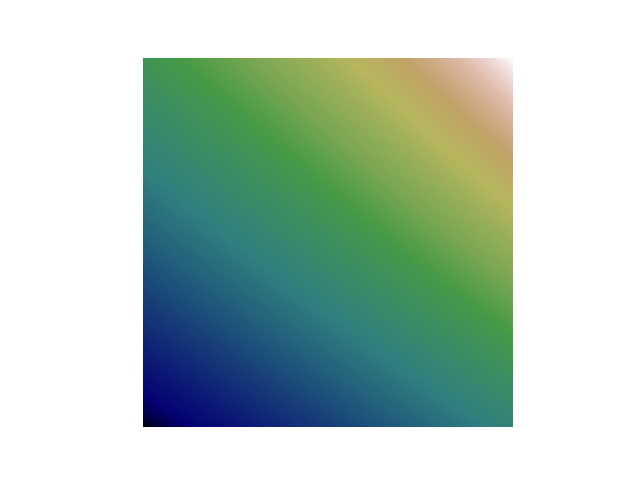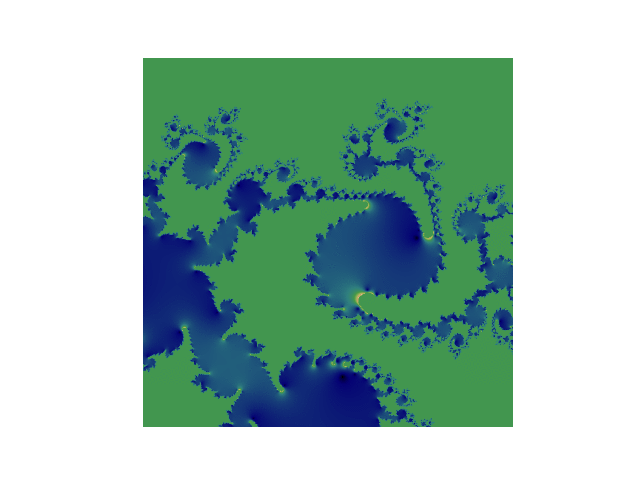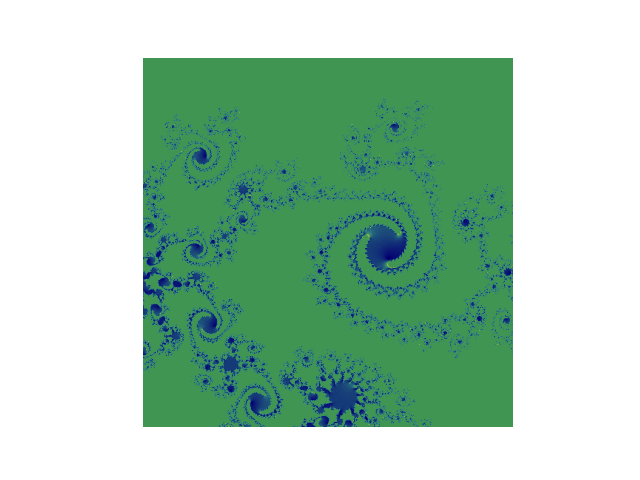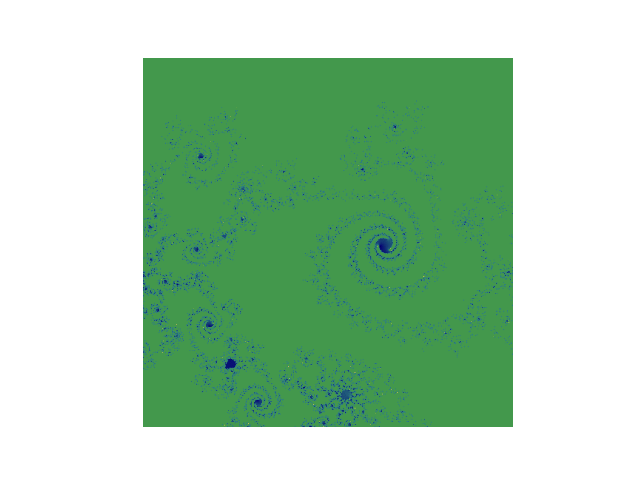
Pour les curieux, pour fabriquer un gif, il faut:
générer chaque image indépendamment de manière numéroté et les sauvegardé à l’aide de
plot.savefig.Utiliser un logiciel pour assembler les images. Dans Linux avec ImageMagick installé: :w
$ convert -delay 10 -loop 0 *.png mandelbrot.gif/bin/sh: 1: $: not foundCela prends pas mal de temps de calcul.
- (Bonus) Ajoutez des jolies images de fractales (voire des images animés) et le code qui les génèrent. Les plus jolies images seront ajoutés pour la postérité au sujet du TD (avec un remerciement).
Exercice 5: Répétition dans une liste
Voici la description d’un problème algorithmique.
- éléments répétés
- Entrée: une liste d’éléments \(L\) et un entier \(k\)
- Retourne: la liste des élément qui apparaissent au moins \(k\) fois.
Par exemple, sur la liste [0, 1, 1, 2, 1, 3, 2]
retournera [0, 1, 2, 3] pour \(k
= 1\), [1, 2] pour \(k=2\) et [1] pour \(k=3\).
Proposez une implémentation impérative et récursive pour ce problème et une analyse de complexité.
Exercice 6: Sous-mots
Pour \(u\) et \(v\) deux mots, on dit que:
\(u\) est un sous-mot de \(v\) si en effaçant des lettres de \(v\) on peut obtenir \(u\).
Par exemple "ab" est un sous mot de "acdb"
mais pas un sous mot de "bcda"
- sous-mot
- Entrée: deux mots \(u\) et \(v\)
- Retourne: Vrai si et seulement \(u\) est un sous-mot de \(v\).
Proposez une implémentation impérative et récursive pour ce problème et une analyse de complexité.
Compiled the: mer. 08 janv. 2025 11:51:09 CET