L2 MIASHS, Algorithme et Programmation 2, année 2021

Arbre binaire de recherche

Un arbre est un objet abstrait souvent manipulé en informatique dans plein de contextes différents.

Un peu de terminologie

Un arbre est un ensemble de noeuds qui peuvent être soit des nœuds internes soit des feuilles. Un nœud interne a un ensemble d’enfants qui sont eux même des arbres.

De nombreux exemples d’arbres sont présents en informatique. Le plus simple à voir c’est votre système de fichiers avec les noeuds internes qui sont les dossiers et les fichiers les feuilles.

On définit plusieurs notions supplémentaires:

• taille la taille d’un arbre est le nombre de nœud qu’il contient.
• branches une branche est une suite de noeuds \(n_0,\ldots, n_p\) tel que \(n_{i+1}\) est un enfant de \(n_i\).
• profondeur la profondeur d’un arbre est la longueur de la plus longue branche.

Des arbres en Python

On définit une notion d’arbre dans ce TD de la façon inductive suivante.

1. Tous les entiers sont des arbres (de taille 1).
2. Une liste d’arbre est un arbre.

Par exemple A = [200, [[32, 25], [52]], 42] donne l’arbre suivant:

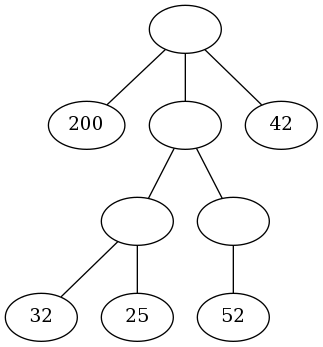
Question 1. Vérifier.

Écrire une fonction est_arbre qui prend un argument et qui retourne si c’est bien un arbre.

Question 2. Taille.

Écrire une fonction taille_arbre qui prend en argument un arbre et qui retourne sa taille.

Question 2. Profondeur.

Écrire une fonction profondeur_arbre qui prend en argument un arbre et qui retourne sa profondeur.

Question 3. Cime.

La cime d’un arbre est la liste de ses feuilles en respectant leur ordre d’apparition. Par exemple, pour l’arbre A, c’est [200, 32, 25, 52, 42].

Proposez une fonction cime.

Des arbres binaires de recherche

Un arbre est un arbre binaire s’il est soit:

• une liste vide
• un entier

ou un arbre vérifiant que:

• un sous-arbre binaire gauche (on parle de fils gauche)
• une feuille
• un sous-arbre binaire droit (on parle de fils droit)

La valeur d’un nœud interne est sa feuille en position 1 dans la liste.

Par exemple [[4, 5, 6], 3, [[1, 20, 30], 2, 44]]

Par exemple [[[], 3, 22], 4, [5, 220, ,[30, 21, []]]]

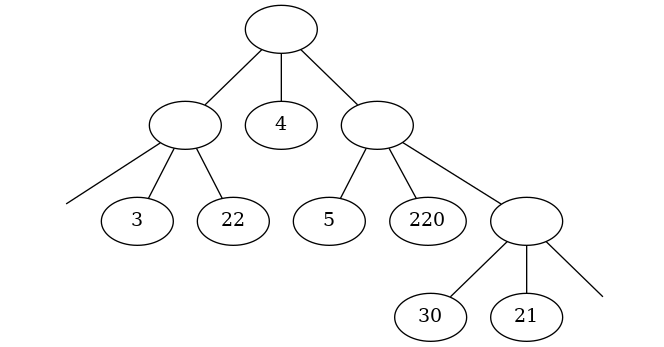
Un arbre binaire est un arbre de recherche si pour chaque nœud les valeurs du sous arbres à droites sont plus petite que la valeur du noeud qui est plus petite que les valeurs du sous-arbre droit.

Par exemple [[4, 5, 6], 10, [[11, 20, 30], 200, 440]]

Question 1. Vérifier.

Écrire une fonction est_ABR qui prend en argument un arbre et vérifie que c’est un arbre binaire de recherche

Question 2. Contient.

Écrire une fonction contient qui prend en argument un arbre et un élément et qui retourne si l’élément est une des valeurs de l’arbre.

Question 3. Ajout.

Écrire une fonction ajout qui prend en argument un arbre binaire de recherche et un entier et qui ajoute en place l’élément à l’arbre.

Question 4. Complexité

Proposez une analyse de complexité pour contient et ajout en fonction de la profondeur de l’arbre.

Compiled the: dim. 07 janv. 2024 23:19:18 CET