Les structures de données

Une structure de données est une manière de stocker des données. Une donnée peut prendre pleins de forme différentes, ça peut être des chaines de caractères, des nombres, des tuples, ou des objets plus complexes.

En Python, on sépare les objets en deux catégories, les objets qui sont mutables (ou modifiable) et ceux qui ne le sont pas (non mutables).

Pour comprendre cette distinction, il faut plonger un peu plus profondément dans la manière de fonctionner de Python (et d’un ordinateur plus généralement).

La gestion de la mémoire

Quand on exécute un programme, on utilise de mémoire vive pour stocker:

• Le code a exécuter
• Des données à utiliser
• De la mémoire de travail

Dans l’absolu, la mémoire vive peux être vu comme un très gros tableau ou chaque case peut prendre une valeur sous forme d’un mot mémoire. Les indices de ce tableau sont appelés des adresses mémoires.

Python manipule cette mémoire et en simplifie énormément la gestion (qui est une tâche de développeur difficile et source de nombreuses erreurs et failles de sécurités). Néanmoins, de nombreuses opérations Python entraîne qu’on utilise de la mémoire, parfois en quantité, sans trop y faire attention.

Par exemple, si on souhaite créer une très grosse de chaîne de caractère:

s = "Une grosse choucroute"*10**15

Traceback (most recent call last):
  File "/var/www/cha/check_py_md", line 77, in repl
    exec(code, env)
  File "<string>", line 1, in <module>
MemoryError

Il n’est pas vraiment possible de savoir ce que Python fait avec la mémoire et c’est rarement intéressant. Néanmoins, on peut récupérer une information sur l’adresse mémoire des objets que Python stock via la fonction de base id.

u = "Je suis une petite choucroute"
print("addresse de u", id(u))

addresse de u 139856289240512

Le nombre retourner par id sert à identifier l’objet Python en tant qu’objet mémoire, mais sans tenir en compte de sa valeur; de sa sémantique. Deux objets Python peuvent être rigoureusement égal, mais avoir deux adresses mémoire différentes:

u = "Je suis un objet quelque part dans la mémoire"*100
v = "Je suis un objet quelque part dans la mémoire"*100
print(id(u) == id(v))

False

Cette égalité peut être testé avec le mot clef is mais il est déconseillé de l’utiliser.

print("égale", u == v)
print("identique", u is v)

égale True
identique False

Pour en savoir plus, un poste de blog intéressant sur ce qu’il se passe derrière.

Mutabilité

Une partie des objets Python ont une propriété importante: ils ne sont pas modifiables. Cela signifie pas qu’on ne peut rien faire avec mais juste que le segment mémoire qui leur est attribué ne vas jamais changer.

Dans ce cas, on dit qu’ils sont non-mutable. C’est le cas de:

• des chaines de caractères
• des tuples
• des nombres (entier, à virgule, ect).

Python est construit autours de cette idée et cela se voit par exemple quand on essaye de modifier une chaîne de caractères:

u = "Je ne suis pas modifiable"
u[0] = "T"

Traceback (most recent call last):
  File "/var/www/cha/check_py_md", line 77, in repl
    exec(code, env)
  File "<string>", line 2, in <module>
TypeError: 'str' object does not support item assignment

Au contraire, certains objets sont mutables, leur addresse en mémoire reste fixe mais leur valeur peut changer. C’est le cas de:

• des listes
• des dictionnaires
• des ensembles

L = []
print(id(L))
L.append(3)
print(id(L))

139856312345792
139856312345792

Il faut faire attention avec les objets mutables car certaines opérations les modifient (ont dit qu’elles sont en place) alors que d’autre créent un nouvel objet. La différence est parfois subtile:

L = []
print(id(L))
L += [3]
print("Je suis en place :)", id(L))
L = L + [4]
print("Pas moi :(", id(L))

139856290891584
Je suis en place :) 139856290891584
Pas moi :( 139856289335744

Quand un objet mutable est en argument d’un appel de fonction, il peut donc arriver qu’on le modifie à l’extérieur de la fonction, ce qui est un comportement à éviter (sauf quand c’est voulu!).

L = [5, 42, 32, 2]

def vilain_tri(L):
    K = []
    while len(L) > 0:
        x = L.pop()
        for i in range(len(K)):
            if x < K[i]:
                K.insert(i, x)
                break
        else: # on va ici si pas de break #rencontrée dans la boucle
            K.append(x)
    return K

K = vilain_tri(L)
print(K) # Le tri marche :)
print(L) # Mais il a effacer ma liste :'(

[2, 5, 32, 42]
[]

On peut beaucoup s’amuser avec la mutabilité. Dans l’absolue, une liste peut prendre tout les objets Python qu’on veut. Donc:

L = []
K = []
L.append(K)
L.append(K) # On peut mettre K deux fois
print(L) # pas de surprise
K.append(3)
print(L) # Oh!

[[], []]
[[3], [3]]

On peut même s’amuser à mettre une liste dans elle même et à la modifier:

L = []
L.append(L)
print(L) # Ça boucle à l'infinie, Python s'en rend compte
L.insert(0, 42)
print(L)
L.insert(0, 32)
print(L)

[[...]]
[42, [...]]
[32, 42, [...]]

Structure de donnée ensemblistes

Il est souvent utile d’avoir une liste d’élément et qu’on souhaite éliminer les répétitions dans un algorithme donnée. Il est toujours possible de le faire à la main, ou utiliser les structures de données ensemblistes.

Formellement, ce sont des représentations d’ensemble d’éléments, c’est à dire, des ensembles d’élément sans répétitions.

On les construit à l’aide du constructeur set en Python. Attention, contrairement aux listes, les ensembles n’ont pas d’ordre sous-jacent

L = [0, 2, 2, 42]
S = set(L)
print(S)

{0, 2, 42}

Que signifie ici sans répétitions ? Est-ce que ça signifie qu’on ne peut pas avoir deux fois le même objets mémoire ou le même objet sémantiquement?

L = ["Une choucroute", "Une choucroute"]
print(id(L[0]) == id(L[1])) # pas les même objets mémoires
S = set(L)
print(S) # un des deux a été enlevé effectivement !

True
{'Une choucroute'}

Quand on essaye d’ajouter à un ensemble une liste, Python n’est pas d’accord:

S = set()
L = [1, 2, 3]
S.add(L)

Traceback (most recent call last):
  File "/var/www/cha/check_py_md", line 77, in repl
    exec(code, env)
  File "<string>", line 3, in <module>
TypeError: unhashable type: 'list'

Par contre, ça ne pose pas de problème d’ajouter un tuple:

S = set()
t = (1, 2, 3)
S.add(t)

La différence provient de la mutabilité. Une liste étant mutable, ce n’est pas évident de dire ce que dois faire un ensemble contenant des liste. Si deux listes sont différentes à un moment données mais sont modifiées et deviennent égales, faut il en supprimer une des deux?

La différence entre mutabilité et non mutabilité, et le fait que les ensembles évitent la répétition, permet de bien meilleurs performances:

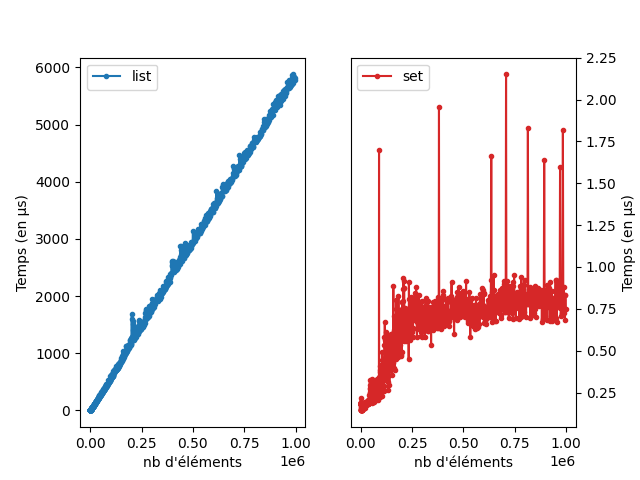
lien vers le code qui a généré l’image

On voit bien que l’appartenance dans une liste est linéaire expérimentalement alors que l’appartenance dans un ensemble est beaucoup plus beaucoup efficace et d’une complexité plus difficile à estimé. Il est en fait en \(O(1)\) et nous verrons comment plus tard.

La différence de performance est certes impressionnante, mais elle n’est pas gratuite. Voici les courbes qui comparent le coût de construction d’une liste par ajout d’élément par rapport à un ensemble.

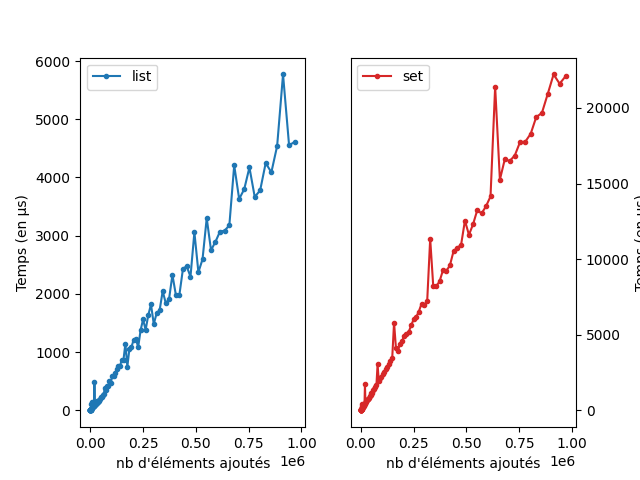
lien vers le code qui a généré l’image

Les ensembles

Derrière l’efficacité des ensembles, se cache une structure de données bien connue et très efficaces: les tables de hachages.

Son fonctionnement se base sur la notion de hachage, c’est à dire, de représentation d’un objet non mutable par un entier. Le hachage est central en informatique à bien des égards (bases de données, cryptographie, cache, algorithmique).

Il existe pleins de manière de construire une fonction de hachage avec des garanties plus ou moins fortes selon les usages que l’on veut faire. Globalement, une propriété des fonctions de hachage importante est l’uniformité.

Pour formaliser ça un peu, on note \(\Omega\) un ensemble fini d’objets a haché. Une fonction de hache d’ordre \(n\) est une fonction \(h\colon\Omega\to [0;n]\).

Uniformité

Une fonction de hache d’ordre \(n\) est presque uniforme si pour \(i\), on a \(\frac{\text{Card}(h^{-1}(i))}{\text{Card}(\Omega)} = \frac{1}{n}\).

On peut adapter cette définition pour que ce soit presque égale.

Réversibilité

Dans certains usage (par exemple cryptographique) on s’intéresse également à la notion de réversibilité d’une fonction de hachage. Il s’agit du problème suivant.

La complexité de cet algorithme dépend fortement de la fonction de hachage. On dit que cette dernière est non-réversible s’il n’existe pas d’algorithme en temps polynomial qui calcul son inverse.

Dans ce cas, on dit que la fonction de hache a des garanties cryptographique. L’existe de fonction de hache avec de tels garanties est une conjecture difficile même si de bonnes candidates existent.

hachages

Python vient avec une fonction de hachages (possiblement réversible!) mais bien pratique.

s = " je suis un objet hachable "
print(hash(s))

317659354037613663

s = "moi aussi!"
print(hash(s))

-3285513902928187524

s = ("moi", ("aussi", ("même", "si", "je", ("suis", "plus"), "compliqué")))
print(hash(s))

7163025506546008313

Et même les très gros entiers:

i = 1234**654
print(hash(i))

1771583243742231625

Évidemment, les éléments mutables ne sont pas hachables

L = ["coucou"]
print(hash(L))

Traceback (most recent call last):
  File "/var/www/cha/check_py_md", line 77, in repl
    exec(code, env)
  File "<string>", line 2, in <module>
TypeError: unhashable type: 'list'

Table de hachage

Une table de hachage est une structure de donnée ensembliste qui permet de stocker et vérifier rapidement si un élément est dans l’ensemble ou non. C’est la structure de donnée qui est derrière les dictionnaire et les ensembles Python et qui justifie leur très bonnes performances.

Une table de hachage c’est:

• Une liste de taille fixée donc chaque cellule est soit vide soit contient un objet quelconque hachable.
• Pour vérifier qu’un élément est dans la table, on calcul son hash modulo la taille de la liste; on obtient ainsi un indice de la liste qu’on va utiliser pour vérifier si l’élément est dedans ou non.
• Quand on ajoute un objet, on regarde le résultat de son hash modulo la taille de la liste. On utilise cette entier comme indice ou insérer l’élément dans la liste.

Il est possible que deux objets se retrouvent dans la même case, dans ce cas on dit qu’il y a une collision. La gestion des collisions est un point crucial des tables de hachages, et nous allons voir ça en détail par la suite.

Les collisions!

Quand on insère un objet dans une table de hachage, il est possible que la place soit prise. Si tout est uniforme et aléatoire, la probabilité pour ça arrive est simple à estimer: \(\frac{n}{T}\) avec \(n\) le nombre d’élément dans la table et \(T\) la taille de la table.

La gestion des collisions peut se faire de beaucoup de manière différentes.

linear probing

Une solution simple a mettre en oeuvre et de chercher la prochaine case vide et d’y mettre l’objet.

L’insertion devient alors:

• On calcul l’indice théorique d’insertion.
• S’il n’est pas libre, on va chercher le prochain indice plus grand de libre et on y met l’objet.

Pour vérifier qu’un objet est dans la table de hachage, il suffit de faire la même chose:

• On calcul l’indice théorique d’insertion.
• On vérifie toutes les cases jusqu’à la prochaine case vide si on y trouve l’objet.

La complexité de l’ajout et la complexité du test d’appartenance dépendent ici de la taille maximal d’élément consécutif dans la table.

Chaînage

Une autre solution simple est d’autoriser le stockage de plusieurs objets dans une case. Dans un langage comme C, on peut associer à chaque case de la table une liste chaînée d’élément.

Quand on ajoute un élément à la table, on l’ajoute à la liste chaînée qui est à la case correspondante. La complexité de l’ajout peut être en \(O(1)\) quelque soit la longueur de la liste chaînée si on s’y prend bien (en stockant un pointeur vers la fin de la liste). Le test d’appartenance lui est en \(O(p)\) avec \(p\) la taille de la liste chaînée la plus longue.

Changement de taille

Quand une table de hachage devient trop remplie, il devient intéressant de changer sa taille. Par exemple, de doubler la taille du tableau sous-jacent. Pour modifier cette taille et garder la structure cohérente, il est nécessaire de recalculer l’indice de chaque élément dans la table.

Le changement de taille nécessite \(O(n)\) opérations, avec \(n\) le nombre d’élément dans la table. Pour garantir un petit nombre de collision, on peut donc doubler la taille de la table dès que le taux de remplissage dépasse une certaine valeur.

Analyse de complexité amortie

La complexité de la structure de données est difficile a analyser. Toutes les opérations d’ajout sont en \(O(1)\) sauf le changement de taille qui est en \(O(n)\). Ce dernier à lieu de temps en temps. On parle de complexité amorti quand on calcul la complexité sur l’ensemble de la durée de vie de la structure de donnée.

Pour simplifier l’analyse de complexité, on va supposer qu’on insère \(n=2^k\) éléments et qu’on double la taille de la table dès que le taux de remplissage dépasse \(50\%\).

Les \(2^k\) insertions vont ainsi engendré \(k\) doublement de table. On peut compter le nombre de fois où chaque élément est insérer. Le premier sera insérer \(k\) fois, les deux suivant \(k-1\) fois, les \(4\) suivant \(k-2\) fois, et ainsi de suite.

Le nombre d’insertions total est donc \(2^k + 2^{k-1} + \ldots + 1 = \sum_{i=0}^k 2^i = 2^{k+1} = 2n\). Si on divise le nombre d’insertions par la complexité total on obtient bien une complexité constante en moyenne bien que ponctuellement (et rarement!), une des insertions peut être très couteuse.

Analyse expérimentale

Si on ajoute de nombreux éléments dans un ensemble en Python, certains ajouts seront très long. Il s’agit des conscéquence de l’implémentation des ensembles via des tables de hachage.

Voici les 30 plus longue insertions dans un ensemble lors de l’insertion de \(10^7\) entiers choisis aléatoirement.

Compiled the: dim. 07 janv. 2024 23:19:16 CET