Les paradigmes algorithmiques

Pour trouver différents algorithmes, on peut s’appuyer sur des grands paradigmes pour être guider. Ces paradigmes peuvent être d’une grande diversité, selon les modèles calculatoires sous-jacent.

Nous allons étudier deux de ces paradigmes parmi les plus commun.

• Diviser pour régner: on décompose le problème en des sous problèmes de tailles plus petites et indépendant, et on assemble le résultat
• Programmation dynamique: on décompose le problème en des sous problèmes de tailles plus petites mais non indépendante, et on va assembler le résultat ET le mémoriser.

Diviser pour régner

Dans la résolution de problèmes algorithmiques, il est parfois possible de diviser l’espace de recherche en plusieurs morceaux disjoints de taille proches, de résoudre récursivement sur chaque morceau le problème et d’assembler les résultats pour l’ensemble. Cette méthode de résolution porte le nom diviser pour régner. Si on en résume les grandes étapes:

1. Trouver une partition du problème en plusieurs morceaux de même taille.
2. Faire un appel récursif pour chaque morceau.
3. Calculer le résultat final en agrégeant le résultat de chaque morceau.

On peut évaluer la complexité du calcul de manière générique en fonction du nombre de morceau (\(k>1\)) et du coût du calcul du résultat final. Si on note \(f(n)\) ce coût, on obtient alors:

\[C_n = k C_{\frac{n}{k}} + f(n)\]

On va distinguer plusieurs cas classique:

Cas 1, \(f(n)=O(1)\).

Dans ce cas, on peut montrer que \(C_n = O(n)\). On le prouve dans un premier temps pour \(n=k^t\) en posant \(F_t = C_{k^t}\).

On a donc, \(F_{t+1} = k F_t + f(k^t)\)

Par hypothèse, il existe \(C\geq 0\), tel que pour tout \(n\), \(f(n)\leq C\) et on a donc \[F_{t+1}\leq k F_t + C\]

La suite \(G_{t}\) définit par récurrence par \(G_{t+1} = k G_t + C\) et \(G_0=F_0\) domine la suite \(F_t\). Il s’agit d’une suite arithmético-géométrique, et on a \(G_t = O(k^t)\).

Pour tout \(n\), il existe \(t\) tel que \(n \leq k^t \leq kn\) donc et donc \[C_n \leq C_{k^t} = F_t \leq G_t = O(kn) = O(n)\]

Cas 2, \(f(n)=O(n)\).

Dans ce cas, on peut montrer que \(C_n = O(n\log n)\).

Comme précédemment, on étudie le cas \(n=k^t\) et on pose \(F_t = C_{k^t}\) et on remarque que \(F_{t+1} = k F_t + f(K^t)\). Il existe une constante \(C\) tel que \(f(n)\leq Cn\) et on a donc \(F_{t+1} \leq k F_t + Ck^t\).

On pose la suite \(G_t\) définit par récurrence par \(G_0=F_0\) et \(G_t = k^t G_0 + tCk^t\). On montre par récurrence que que cette suite domine la suite \(F_t\). En effet, \(G_{t+1} = k^{t+1} G_0 + (t+1) Ck^{t+1} = k(k^t G_0 + tCk^t) + Ck^{t+1} = k G_t + tCk^t\). \(F_{t+1} \leq k F_t + Ck^t \leq k G_t + Ck^t = G_{t+1}\).

Hors, \(G_t = O(tk^t)\).

Pour tout \(n\), il existe \(t\) tel que \(n\leq k^t \leq kn\) et donc \[C_n \leq C_{k^t} = F_t \leq G_t = O(tk^t)\]

Comme \(t\) est le logarithme en base \(k\) de \(n\), on a que \(t = \frac{\log n}{\log k}\) et donc \(tk^t= O(n\log n)\).

Un exemple, le cas du max

On va reprendre le problème de la fonction max vu dans les deux derniers cours pour illustrer une approche diviser pour régner. La complexité obtenue ne sera pas meilleur, mais ça permettra d’illustrer la méthodologie

Rappel:

On va diviser la liste en deux, chercher le max dans chaque partie et assembler le résultat. Cela donne une définition récursive:

def max_divise_regner(L):
    n = len(L)
    if n == 1:
        return L[0]
    m1 = max_divise_regner(L[:n//2])
    m2 = max_divise_regner(L[n//2:])
    return max(m1, m2)

On peut vérifier sur un exemple que ça marche bien:

print(max_divise_regner([0, 42, 3, 4, 5]))

42

Analyse de complexité (algorithmique)

Si on note \(C_n\) la complexité de l’algorithme max_divise_regner pour \(n\) la taille de la liste, alors on a la relation de récurrence:

\[ \begin{cases} C_{2n} &= 2C_n + 3\\ C_{2n+1} &= C_n + C_{n+1} + 3 \end{cases} \]

En posant \(F_n = C_{n+1} - C_n\) alors on a que \[ \begin{cases} F_{2k} &= C_k + C_{k+1} + 3 - (2C_k + 3) &= C_{k+1} - C_k = F_k&\text{(cas $n=2k$ est paire)}\\ F_{2k+1} &= 2C_{k+1} + 3 - (C_{k+1} + C_{k} + 3) &= C_{k+1} - C_k = F_k&\text{(cas $n=2k+1$ est impare )} \end{cases} \]

On a donc dans tous les cas \(F_n\) est constante égale \(F_1=C_2 - C_1\) avec \(C_1=2\) et \(C_2= 2C_1 + 3=7\), et donc F_n=5$. On a donc que \(C_{n+1} = C_n+5 = 5n+2\), ce qui donne une complexité en \(O(n)\) (comme prévu).

Analyse de complexité (adapté à Python)

Nous avons considéré ici que l’opération \(L[:n//2]\) n’était pas couteuse, hors cette opération réalise une copie complète de la liste jusqu’à \(n//2\). On peut le vérifier facilement expérimentalement:

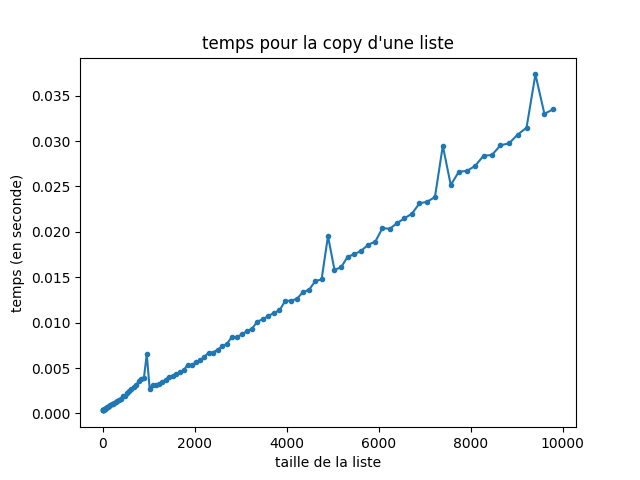
lien vers le code qui a générer l’image

Avec les copies, l’analyse de complexité et beaucoup moins bonne, on obtient en effet:

\[ \begin{cases} C_{2n} &= 2C_n + 2n + 3\\ C_{2n+1} &= C_n + C_{n+1} + 2n + 4 \end{cases} \]

En posant \(F_n = C_{n+1} - C_n\) alors on a que \[ \begin{cases} F_{2k} &= C_k + C_{k+1} + 2n + 4 - (2C_k + 2n + 3) &= C_{k+1} - C_k + 1 &= F_k + 1&\text{ (cas $n=2k$ est paire) }\\ F_{2k+1} &= 2C_{k+1} + 2n + 5 - (C_{k+1} + C_{k} + 2n + 4) &= C_{k+1} - C_k + 1 &= F_k + 1&\text{ (cas $n=2k+1$ est impaire) } \end{cases} \]

Ça nous donne que \(F_n = \log_2(n)\) et donc \(C_{n+1} = C_n + \log{n}\) et que \(C_n = \sum_{i=0}^n \log(i) = \log(n!)\) On peut utiliser la formule de Stirling ce qui nous donne que \(C_n = \log(\sqrt(2\pi n)(\frac{n}{e})^n) = C.\log(n) + n\log(\frac{n}{e}) = O(n\log n)\).

Implémentation en Python sans copie de liste

Il est en faite possible de fournir une implémentation qui évite les copies de liste inutile. On va donc refaire une implémentation, en représentant les sous liste par des des paires d’entiers.

def max_divise_regner2_aux(L, a, b):
    """ Retourn le max de L entre a et b """
    if a + 1 == b:
        return L[a]
    point_median = a + (b - a)//2
    m1 = max_divise_regner2_aux(L, a, point_median)
    m2 = max_divise_regner2_aux(L, point_median, b)
    return max(m1, m2)

def max_divise_regner2(L):
    return max_divise_regner2_aux(L, 0, len(L))

print(max_divise_regner2([0, 12, 3, 4, 5, -10]))

12

On peut mesurer les différentes implémentations:

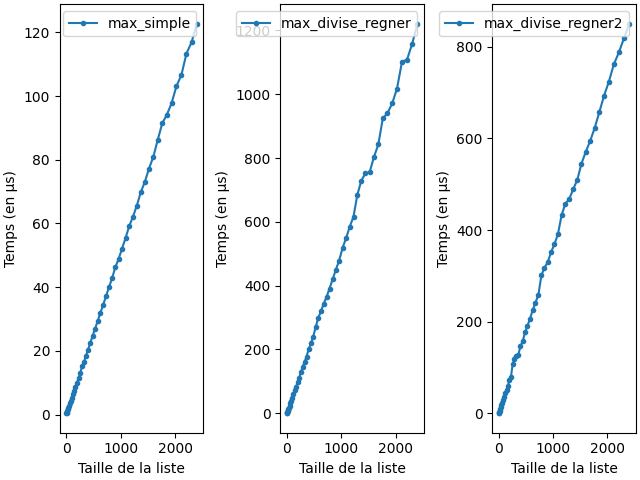
liens vers le code qui a générer l’image

Les tris !

Le problème du tri d’une liste (d’entier) est l’un des problèmes algorithmiques les plus anciens de l’informatique. Ces problèmes sont utilisés partout. Dans les grosses bases de données, dans beaucoup d’algorithmes utilisés au quotidiens, dans des problèmes de routage.

Le tri par insertion

Un algorithme très simple pour le tri:

def tri_insertion(L):
    if len(L) <= 1:
        return L
    m = max(L)
    L.remove(m)
    K = tri_insertion(L)
    K.append(m)
    return K

On vérifie que ça marche sur un exemple:

L = [0, 42, 3, 27]
print(tri_insertion(L))

[0, 3, 27, 42]

Il est possible d’en faire une version iterative:

def tri_insertion_iterative(L):
    K = []
    while L:
        m = min(L)
        L.remove(m)
        K.append(m)
    return K

On vérifie que ça marche sur un exemple:

print(tri_insertion_iterative(L))

[0, 3, 27, 42]

Analyse de complexité

La version récursive et itérative ont la même complexité qui dépend de la complexité de l’opération remove sur les listes. Cette dernière peut nécessiter de recopier la liste entièrement (ce qui est en \(O(n)\) où \(n\) est la taille de la liste). On obtient donc: \(C_{n+1} = 2n + 1 + C_n\) avec \(C_1 = 1\) et donc

\[C_n = 1 + \sum_{i=2}^n(2i+1) = 1 + 2\sum_{i=2}^n i + (n-2) = n-3 + \sum_{i=1}^n i = n-3 + n(n-1) = O(n^2)\]

Les deux implémentations qu’on propose ne sont pas en place: elle stock le résultat dans un tableau intermédiaire. Il est possible de faire bien mieux en modifiant la liste directement.

def argmax(L, maxsize=None):
    """
    Retourne l'indice où on trouve la
    première occurrence de la valeur maxisum
    de la liste jusqu'à maxsize.
    """
    n = maxsize if maxsize else len(L)
    arg = 0
    maxv = 0
    for i in range(n):
        if L[i] > maxv:
            arg = i
            maxv = L[i]
    return arg

Par exemple:

L = [0, 4, 5, 42, 3, 4]
print(argmax(L))
print(argmax(L, maxsize=3))

3
2

Avec cette fonction, on peut améliorer le tri par insertion:

def tri_insertion_iterative2(L):
    n = len(L)
    for i in range(n):
        j = argmax(L, maxsize=n-i)
        L[j], L[n-i-1] = L[n-i-1], L[j]

On vérifie que ça marche sur un exemple. Remarquez qu’on n’affiche pas le résultat de la fonction, mais la même liste initial, qui a été modifié (en place).

tri_insertion_iterative2(L)
print(L)

[0, 3, 4, 4, 5, 42]

Analyse expérimentale

On peut regarder les performances des différents tris en pratique:

lien vers le code qui a généré l’image

Le tri fusion

Nous allons proposer un meilleur algorithme de tri, basé sur diviser pour régner. L’idée principal et de couper le tableau en deux. De trier la partie gauche, trier la partie droite et de fusionner le résultat.

def tri_fusion(L):
    n = len(L)
    if n <= 1:
        return L
    K1 = tri_fusion(L[:n//2])
    K2 = tri_fusion(L[n//2:])
    # On fusionne
    resultat = []
    while bool(K1) and bool(K2):
        # Tant que les deux listes sont non vides
        if K1[0] > K2[0]:
            resultat.append(K2.pop(0))
        else:
            resultat.append(K1.pop(0))
    if K2:
        resultat.extend(K2)
    if K1:
        resultat.extend(K1)
    return resultat

Comme d’habitude, on vérifie sur un exemple que ça marche:

L = [0, 42, 3, 7, 9, 21, 1, 9, 0]
print(tri_fusion(L))

[0, 0, 1, 3, 7, 9, 9, 21, 42]

Analyse de complexité

En posant \(C_n\) la complexité, on a:

\[ \begin{cases} C_{2n} &= 2C_{n} + 2 + 2n\\ C_{2n+1} &= C_n + C_{n+1} + 2 + 2n \end{cases} \] avec \(C_1 = 2\).

En posant \(F_n = C_{n+1} - C_n\), on a

\[ \begin{cases} F_{2n} &= C_{2n+1} - C_{2n} &= C_n + C_n{n+1} + 2 + 2n - (2C_n + 2 + 2n) &= C_{n+1} - C_n&=F_n\\ F_{2n+1} &= C_{2(n+1} - C_{2n+1} &= 2C_{n+1} + 4 + 2n - (C_n + C_{n+1} + 2 + 2n) &= C_{n+1} - C_n + 2 &= F_n + 2 \end{cases} \]

De plus, un simple calcul montre que \(F_1 = C_2 - C_1 = 6\).

On prouve que \(F_n = 2k + 4\) où \(k\) est le nombre de \(1\) dans la décomposition binaire de \(n\) que l’on note \(|n|_2\).

Comme \(F_1 = 2\times 1 + 4 =6\), le cas de base (\(n=1\)) est immédiat.

On suppose que le résultat est vrai pour tout entier jusqu’à \(n\) et on le montre pour \(n+1\).

• Si \(n\) est impaire, alors \(n+1\) est paire et le nombre de bits dans la décomposition binaire de \(n+1\) est le même que dans la décomposition binaire de \(n\) (on a \(|n+1|_2=|n|_2\)) et donc on a bien \(F_{n+1} = F_{\frac{n+1}{2}\).

• Si \(n\) est paire, alors \(n+1\) est impaire et \(F_{n+1} = F_{\frac{n}{2}} + 2\). Or \(|n+1|_2 = |\frac{n}{2}|_2 +1\) et donc \(F_{n+1} = 2|\frac{n}{2}|_2 + 4 + 2 = 2|n+1|_2 + 4\), ce qui conclu la preuve.

Finalement, on a que \[C_n = \sum_{i=0}^n F_i = 4n + 2\sum_{i=0}^n |i|_2\]

Or, on remarque que \(|i|_2 \leq \log_2 n\) et donc que \(C_n = O(n\log(n))\).

Analyse Expérimentale

On peut regarder les performances des différents tris vu jusqu’à présent qu’on compare au tri implémenté par défaut dans Python:

lien vers le code qui a généré l’image

On remarque que les allures des courbes des tris Fusion et de Python sont similaires. Le tri par insertion est plus efficaces que le tri fusion pour de petites valeurs de liste, mais le dépasse rapidement quand la taille de la liste grossi.

Selection

Voir ici

Compiled the: mer. 04 sept. 2024 12:49:59 CEST