Rappels en Python

• Python est un langage de programmation interprété: il est exécuté dans une machine virtuelle
• D’autres langages sont compilés directement en langage machines (par exemple le C)

Un langage interprété est généralement moins performant (on exécute un code non optimisé) mais plus simple à écrire (pas besoin de modifier le code pour des machines différentes). Un code Python sera exécutable sur toute machine pouvant exécuter la machine virtuelle Python/.

• Python permet de compenser sa faible performance par des structures de données très efficaces.

L’objectif de ce cours est de comprendre cette notion d’efficacité plus finement.

Interagir avec la machine virtuelle Python

Il y a trois manières pour écrire du code en Python:

• Dans un fichier texte (avec un éditeur quelconque). Puis on exécute le code avec la commande python

$ python monfichier.py

• Avec la console interactive en lançant le programme python sans argument. Il est possible d’avoir une console interactive plus agréable à l’aide de la commande ipython (pour interactive python)

ipython ajoute notamment l’auto-complétion qui est d’une bonne aide.

• Avec les notebook jupyter en tapant jupyter notebook. Les notebooks permettent de construire du code lisible, avec des commentaires textuels et une intégration de pour les mathématiques.

Quand utiliser quoi

Pour essayer des petits morceaux de codes, les consoles interactives sont très pratiques. Pour écrire un code long, et des fonctions, il est préférable d’utiliser un éditeur de texte adapté (avec ou sans intégration de Python). Pour les rendus et travailler à plusieurs, les notebook sont utiles car ils permettent de soigner la forme, de revenir en arrière (mais cela prend du temps de faire ça bien).

La documentation

Apprendre à programmer c’est avant tout pouvoir lire la documentation et être autonome pour apprendre de nouveaux concepts. Il n’y a pas de fin à ce qu’on peut apprendre et il est normal d’oublier ce qu’on à appris. Par contre, il est indispensable de pouvoir trouver l’information rapidement, et savoir l’utiliser de manière approprier.

La documentation Python est la source principale d’information à avoir toujours ouverte. Suivre le tutoriel est une excellente idée, en reprenant les exemples.

Algorithmique

Programmer c’est transformer une description informelle d’un problème en un code que la machine exécute. Un programmeur doit se demander:

1. Comment l’écrire pour que ce soit facile à lire et à modifier
2. Comment l’écrire pour que ce soit efficace
3. Est-ce que mon code fait ce qu’il faut

Il est quasiment impossible d’écrire un algorithme correctement du premier coup, il faut donc toujours tester son code sur des exemples, et vérifier si on a bien traité tous les cas.

L’algorithmique s’intéresse à comment faire des algorithmes efficaces pour des problèmes donnés. C’est un domaine de recherche autant que de pratique industriel. Même des sujets très étudiés (par des générations d’étudiants) comme le tri d’un tableau sont encore le sujet de recherche.

Efficacité des algorithmes

L’efficacité d’un algorithme dépend de la mesure. Quand on est exécute un programme python on s’intéresse souvent au temps de calculs autrement dit la rapidité de l’exécution du programme. C’est une première mesure intéressante.

On prends l’exemple du problème contient:

Une implémentation évidente de ce problème:

def contient(L, e) -> bool:
    """ vérifie que e est dans L """
    for s in L:
        if e == s:
            return True
    return False

from typing import Iterable, Any
def contient(L: Iterable, e: Any) -> bool:
    """ vérifie que e est dans L """
    for s in L:
        if e == s:
            return True
    return False

from typing import List
def contient(L: List[int], e: int) -> bool:
    """ vérifie que e est dans L """
    for s in L:
        if e == s:
            return True
    return False

La vitesse d’exécution du programme est immédiatement proportionnelle au nombre d’étape de calcul du programme. Ici il s’agit du nombre de fois où la condition s == n est vérifiée. Ce nombre varie en fonction de \(L\) et de \(e\), il faut donc déterminer la vitesse d’exécution en fonction des variables.

Par exemple, pour la liste L = list(range(1000)), le nombre d’étape pour L et l’entier 123 est \(123\) mais pour l’entier -1 le nombre d’étape est \(1000\).

La complexité dépend des opérations atomiques qu’on s’autorise. Par exemple, en Python la multiplication de deux entiers peut prendre du temps (car les entiers sont de taille non bornée, contrairement à d’autres langages) mais la plupart du temps on ne l’utilise que sur des petits entiers et on la considère comme constante.

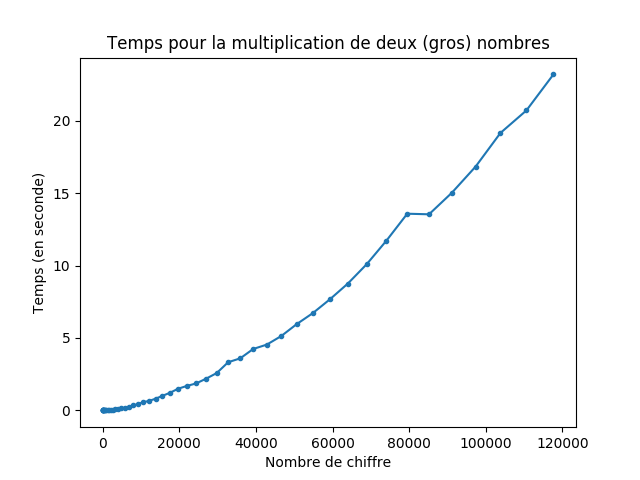
lien vers le code qui a généré l’image

La complexité dépend donc toujours:

1. Du modèle de calcul
2. Des opérations atomiques qu’on considère
3. Des paramètres qu’on prend en compte.

Complexité au pire cas

On parle de complexité au pire cas quand on évalue la complexité dans la pire situation possible en fonction d’un ou plusieurs paramètres du problème. La complexité au pire cas pour contient en fonction de la taille de la liste \(n\) est donc \(n\).

Complexité en moyenne

On parle de complexité en moyenne quand on évalue la complexité en moyenne en fonction d’une distribution donnée de ses entrées. Évaluer la complexité en moyenne d’un algorithme peut être très difficile. En pratique, on peut l’évaluer expérimentalement en utilisant une distribution uniforme.

La distribution uniforme peut ne pas rendre compte de certaines classes d’instances très importantes, donc c’est une notion à manier avec beaucoup de précautions.

Quelques exemples

Exemple 1. max

Voici deux implémentations du problème max

Implémentation 1

def est_max(L: List[int], m:int) -> bool:
    """ vérifie que m est l'élément maximal de L """
    for e in L:
        if e > m:
            return False
    return contient(L, m)

def max1(L: List[int]) -> int:
    """ retourne l'élément le plus grand de la liste """
    for e in L:
        if est_max(L, e):
            return e

Implémentation 2

def max2(L: List[int]) -> int:
    """ retourne l'élément le plus grand de la liste """
    if len(L) == 0:
        return
    m = L[0]
    for i in range(1, len(L)):
        e = L[i]
        if e > m:
            m = e
    return m

Analyse de complexité

On note \(n\) la longueur de la liste \(L\). Dans la première implémentation, la fonction max fait \(n\) appels à la fonction est_max qui est de complexité \(2n\) au pire cas, qui est atteint si \(L\) est une liste triée. On aura donc \(2n^2\) étapes dans le cas d’une liste triée. Dans la deuxième implémentation, on doit tester si la liste est non vide et, au pire cas, on réalise à la fois la condition et l’affection à chaque tour de boucle (si la liste est triée) et donc nécessite \(2n + 1\) étapes.

La différence est très visible:

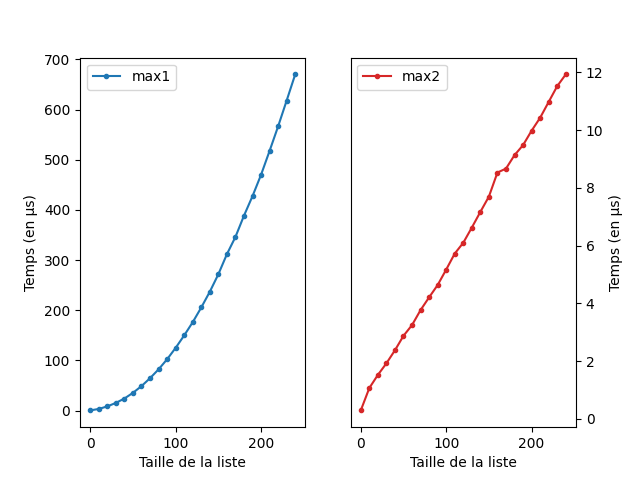
lien vers le code qui a généré l’image

lien vers le code des fonctions

Notations de Landau

La complexité est souvent considérée uniquement de manière asymptotique. On la note alors à l’aide des notations de Landau qu’il est indispensable de connaître.

Les notations sont par exemples utilisés dans le wiki de la complexité des structures de données de python.

Typiquement, on considère que la complexité de max est \(O(n)\) (linéaire), sans se préoccuper des constantes multiplicatives et additives.

Exemple 2: unique

Voici deux implémentations du problème uniquelist

Par exemple, la liste L=[0, 2, "a", 2, "a"], on a que uniqueliste(L) retourne [0, 2, "a"]

Implémentation 1

def uniquelist(L: List) -> List:
    """  une liste contenant les éléments de $L$ sans répétition et dans l'ordre d'apparition """
    K = []
    for e in L:
        if not e in K:
            K.append(e)
    return K

Implémentation 2

def uniquelist(L: List) -> List:
    """  une liste contenant les éléments de $L$ sans répétition et dans l'ordre d'apparition """
    K = []
    S = set()
    for e in L:
        if not e in S:
            K.append(e)
            S.add(e)
    return K

Analyse de complexité

On fixe \(n\) la longueur de la liste \(L\). On évalue la complexité en fonction de \(n\). Dans chaque implémentation, on fait \(n\) tour de boucles en parcourant la liste. Comme dans l’exemple précédant, il faut évaluer le coût de chaque boucle. On peut vérifier dans la documentation de Python la complexité des opérations e in K (appartenance dans une liste) et e in S appartenance dans un ensemble, ainsi que des opérations K.append(e) (ajout à une liste) et S.add(e) ajout dans un ensemble.

D’après le wiki de python:

• e in K à une complexité \(O(n)\)
• e in S à une complexité \(O(1)\)
• K.append(e) à une complexité \(O(1)\)
• S.add(e) à une complexité en moyenne \(O(1)\) en pratique on considère que cette opération est en \(O(1)\)

On a donc la première implémentation qui a une complexité au pire cas \(O(n^2)\) et la seconde une complexité \(O(n)\).

Exemples d’algorithmes du texte

On rappelle le fonctionnement des chaînes de caractères.

Pour une chaîne de caractères (str) s, on rappelle que:

• s[i] est la ième lettre de la chaîne (c’est aussi une chaîne de longueur \(1\)) Par exemple:

chaine = "Le chocolat chaud, c'est bon"
print(chaine[4])

h

• Il est possible d’itérer sur les chaînes de caractères Par exemple

chaine = "Pizza"
for lettre in chaine:
    print(lettre)

P
i
z
z
a

Découpage de chaîne

Étudions l’algorithme:

Une implémentation simple:

def decoupe(s: str, i: int, j: int) -> str:
    """ retourne la chaîne entre les positions i et j de s """
    resultat = ""
    for k in range(i, j):
        resultat += s[k]
    return resultat

Par exemple, on a:

s = "La crème aux marrons"
print(decoupe(s, 0, 7))
print(decoupe(s, 3, 8))

La crèm
crème

Analyse de complexité:

Si on pose comme paramètre \(n:= j-i\), alors la complexité de decoupe est en \(O(n)\).

Comparaison expérimental

On peut comparer l’efficacité de la version Python et de celle qu’on a faite à la main. On voit que les deux se comportent linéairement mais que la version python est plus efficace d’un facteur \(1000\).

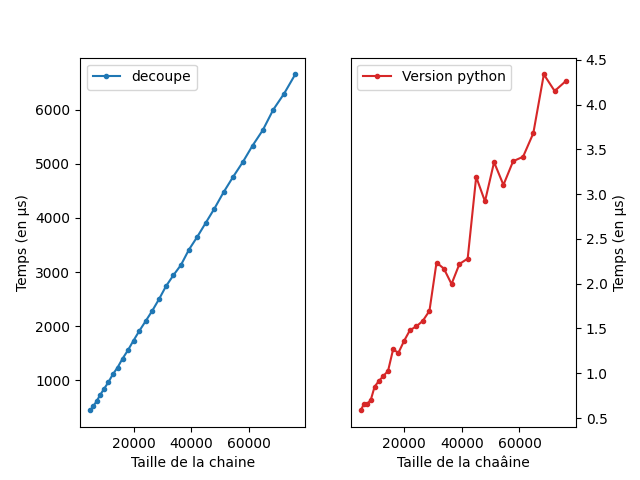
lien vers le code qui a générer l’image

Exemple 3. Sous-chaine

Implémentation

On introduit une première fonction auxiliaire qui vérifie que \(s\) commence par \(t\).

Pour implémenter cette fonction, on peut simplement faire:

def commence(s: str, t: str) -> bool:
    """ Retourne True si s commence par t """
    q = len(t)
    if len(s) < q:
        return False
    for i in range(q):
        if s[i] != t[i]:
            return False
    return True

Une autre manière, plus optimisée mais avec la même complexité:

def commence2(s: str, t: str) -> bool:
    """ Retourne True si s commence par t """
    q = len(t)
    return s[:q] == t

Ici, le symbole d’égalité == cache en faite la boucle faite dans commence. Elle est implémenté de manière beaucoup plus efficace néanmoins (car elle court-circuite la machine virtuelle Python).

On peut maintenant facilement écrire sous chaine.

def sous_chaine(s, t):
    """
    Retourne la position ou t apparait dans s pour la première fois,
    ou None si elle n'existe pas.
    """
    n = len(s)
    for i in range(n):
        if commence(s[i:], t):
            return i
    return None

Analyse de complexité

Ici, l’analyse dépend de deux paramètre, la taille de \(s\) et la taille de \(t\). On suppose que les appels à len sont constant (ce qui est raisonnable en Python, mais pas en C par exemple).

On va donc avec une notion de complexité qui dépend de \(n\), la taille de \(s\) et de \(q\), la taille \(t\).

Dans le pire cas, on fait \(n\) tour de boucle et a chaque tour de boucle on exécute la fonction commence au complet.. Le nombre d’instructions est donc \(q\) sauf pour les \(q\) derniers tours de boucle ou le nombre d’instruction est \(3\) car le premier argument à une taille plus petit que \(q\). On a donc \((n-q)q + 3q\) ce qui donne \(O(nq)\) comme complexité.

Pour justifier que ceci est réaliste, on veut exhiber des exemples de mots \(s\) et \(t\) permettant d’attendre ce nombre d’instructions. Si les mots sont trop différents, par exemple s="aaaaaaaaaaa" et t="bbbbb", alors la fonction commence aura toujours une complexité en \(O(1)\). Si les mots sont trop proches, il sera dure d’éviter que \(t\) soit un sous-mot de \(s\).

En fait, on peut même prouver que le nombre d’instruction \((n-q)q + 3q\) n’est pas réellement atteignable. En effet, si au premier tour de boucle commence retourne False à la toute fin, ça signifie que \(s=pas'\) et \(t=pb\) avec \(p\) un mot de taille \(q-1\) et \(a\) et \(b\) deux lettre quelconque et \(s'\) un mot quelconque.

Mais on a donc qu’au \(q\) tour de boucle, la fonction commence va éxécuter au plus \(3\) instructions.

Néanmoins, si on prends comme exemple pour \(s\) le mot \(aaaa\cdots\) de taille \(n\) et pour \(t\) le mot \(aaa\cdots ab\) de taille \(q\), alors le nombre d’instruction pour sous_chaine sera \(\frac{n}{q}\sum_{i=0}^q i\). Comme \(\sum_{i=0}^q i=\frac{q(q-1)}{2}\) et on obtient alors un nombre d’instructions \(\frac{n}{q}\cdot\frac{q(q-1)}{2} = \frac{n(q-1)}{2} \in O(nq)\)

Analyse expérimentale

On réalise la version expérimentale où sous_chaine1 est la version en pure Python, sous_chaine2 celle qui utilise la sous-fonction commence2 et sous_chaine3 la version optimisée fournie Python qui utilise la méthode index des chaînes de caractères. La version optimisée semble être linéaire mais il faudrait regarder des valeurs plus grandes. Les mots utilisés sont \(u:=a^{2n}\) et \(v:=a^nb\).

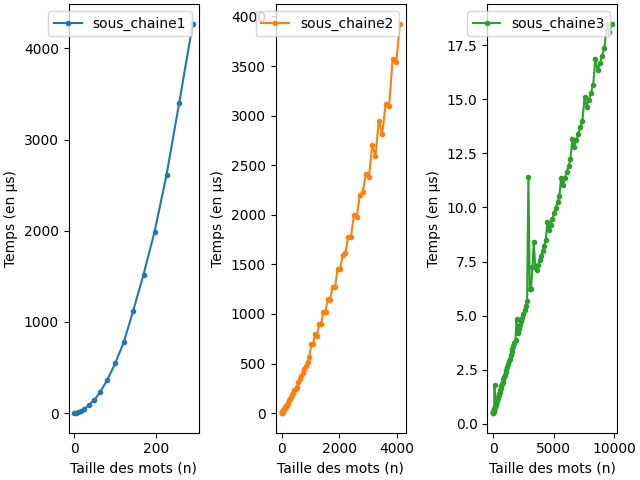
lien vers le code qui a générer l’image

Autres exemples (à reprendre à la maison)

• La complexité de l’addition apprise à l’école a une complexité en \(O(n)\) où \(n\) est le nombre de chiffres.
• La complexité de la multiplication apprise à l’école a une complexité en \(O(n^2)\) où \(n\) est le nombre de chiffres (mais on peut faire mieux).
• La complexité de exponentiation \(a^n\) apprise à l’école à une complexité en \(O(n)\) (mais on peut faire mieux).
• La complexité du tri par insertion

Complexité en espace, Complexité parallèle et complexité distribué

Dans certaines situations, les notions de complexité en temps ne sont pas pertinentes. Par exemple, il peut arriver qu’un algorithme nécessite trop de mémoire mémoire vive pour être utilisé ce qui rend un algorithme non utilisable quand bien même il est efficace. Il est alors important d’avoir une notion de complexité qui prenne en compte l’espace mémoire utilisé et pas uniquement le temps: c’est le rôle de la complexité en espace. Certains problèmes peuvent bénéficier grandement du fait que les processeurs peuvent exécuter plusieurs tâches en parallèle. Pour mesurer la complexité dans ce contexte, on parle alors de complexité parallèle. Dans d’autres situations, paralléliser le calcul ne suffit pas, il faut alors le distribuer sur plusieurs machines (parfois des centaines!). Le goulot d’étranglement peut alors devenir la communication réseau entre les machines et pas le calcul localement sur chaque machine, et on parle alors de complexité distribuée.

Compiled the: mar. 17 déc. 2024 14:03:17 CET