Fonctions et récursivités

Il y a plusieurs grands paradigmes de programmation qu’il faut connaître au moins superficiellement:

• La programmation impérative: il s’agit de celle apprise en faisant du Python standard, avec des séquences d’instructions, des instructions de contrôle de flots, des boucles des variables, des appels de fonctions. Ce type de programmation est très proche du langage machine.

• La programmation fonctionnelle: il s’agit d’un paradigme centré autours de l’exécution de fonction, sans boucle et des primitives permettant de composer et de manipuler les fonctions. Ce paradigme est particulièrement adapté aux problèmes d’accès concurrents aux ressources, là où la programmation impérative devient justement très problématique. Il est par exemple simple de paralléliser un programme fonctionnel.

• La programmation par objet: dans ce paradigme, le programmeur définit et manipule des objets complexes afin de découper le programme en des unités plus simple et indépendantes. Cela permet d’introduire des couches d’abstractions supplémentaire, de factoriser le code, et de l’écrire de manière collaborative efficacement.

Il y a beaucoup d’autre paradigme, (par exemple la Programmation asynchrone très utilisée dans les langages du web).

Aujourd’hui on va aborder la récursivité et (un peu) de programmation fonctionnelle en Python.

Retour sur les fonctions et sur la portée des variables en Python

En Python, on connait une manière de définir les fonctions (vu dans le premier TD):

def ma_fonction(un_argument, un_autre, une_clef="valeur par défaut"):
    """ Courte description de la fonction

    Longue longue description de la fonction, doit contenir
    plein d'information intéressante, incluant la complexité,
    le type d'algorithmes, des pointeurs vers des pages (wikipédia
    par exemple).

    Variables
    ---------
    un_argument : int
        On indique ici le type de variable attendu et une courte description
    un_autre : str
        on le fait pour chaque variable

    Retourne
    --------
    Une chaîne de caractères (str)

    Exemples
    --------
    On ajoute des exemples d'execution qui illustre comment la fonction
    marche.

    >>> ma_fonction(5, "m", une_clef=" une chouquette!")
    mmmmm une chouquete à la crème
    """
    return un_autre * un_argument + une_clef

Quand la machine virtuelle Python lit ce bout de code, elle charge dans l’espace de nom la fonction (sans exécuter son code). Ce code peut d’ailleurs dépendre de variable extérieur. Par exemple:

def f1():
    print(v)
v = 3
f1()

3

Si on change la variable:

v = "chouquette"
f1()

chouquette

La variable v ici utilisé dans la fonction f1 est considéré par Python comme globale (à l’extérieur de la fonction).

Par contre, si on exécute

def f2():
    v = "millefeuille"
    print(v)
v = 3
f2()

millefeuille

Cette fois-ci en changeant la variable:

v = "chouquette"
f2()

millefeuille

Il est possible d’indiquer à Python qu’on souhaite que v soit considéré comme une variable globale:

def f3():
    global v
    print(v)
    v = "millefeuille"
v = 3
f3()

3

La variable v a été changé par la fonction:

print(v)

millefeuille

Il est très déconseillé de recourir à des variables globales ainsi, sauf très rare exceptions (ajustement de méta variables de contrôle du programme par exemple)

Manipulation de fonctions

Lorsqu’on définit une fonction avec le mot clef def elle peut être manipulée comme n’importe quel objet Python. En particulier on peut la stocker dans une variable, la passer en argument à une fonction, les stocker dans des listes, ect…

def patisserie():
    return "éclaire au chocolat"
x = patisserie
print(x())

éclaire au chocolat

On peut aussi ajouter des fonctions à des listes:

def viennoiserie():
    return "croissant"

L = [patisserie, viennoiserie, patisserie, viennoiserie]
s = ""
for x in L:
    s += x() + " "
print(s)

éclaire au chocolat croissant éclaire au chocolat croissant

Et on peut même passer une fonction en argument à une autre fonction:

def afficheur(une_fonction):
    """ Affiche le résultat d'une fonction """
    print(une_fonction())

afficheur(viennoiserie)

croissant

La récursivité

Nous avons vu que des fonctions pouvaient être manipulées au premier ordre, c’est à dire comme des variables, et passer en argument d’autres fonctions. Lorsqu’on définit une fonction, son symbole est chargé dans l’espace des noms et il est utilisable dans tous code qui suit. En particulier, il est utilisable dans son propre code.

def chouquette(n):
    if n == 0: # initialisation
        return " chouquette"
    if n > 0: # étape d'induction
        return "m" + chouquette(n-1)
print(chouquette(5))

mmmmm chouquette

Ici, l’appel à la fonction chouquette dans chouquette ne pose pas de problème puisque la fonction est déjà définie. Cela va simplement relancer le code en modifiant l’argument. On dit alors que la fonction chouquette est définie de manière récursive.

Tout programme peut être écrit de manière récursive (on peut toujours supprimer les boucles, pour les remplacer par des appels de fonctions récursif) mais parfois utiliser des boucles est plus simple, parfois des fonctions récursives sont plus pratiques.

Un programme récursif doit toujours:

• Avoir une condition initiale qui permet de garantir que le programme ne va pas boucler à l’infinie
• Un cas général

Comprendre les fonctions récursive

Les fonctions récursives sont parfois difficile à appréhender. Pour bien comprendre comment une fonction récursive fonctionne, il est utile de dérouler l’arbre d’appel à la main sur des petits exemple. Par exemple, pour la fonction chouquette on peut calculer pour chaque valeur de n la valeur de retour par ordre croissant:

def chouquette(n): # Pour n = 0
    if n == 0: # Vrai !
        return " chouquette"
        # Valeur de retour: " chouquette"
    if n > 0: # étape d'induction
        return "m" + chouquette(n-1)

def chouquette(n): # Pour n = 1
    if n == 0: # Faux
        return " chouquette"
    if n > 0: # Vrai !
        return "m" + chouquette(n-1)
        # Valeur de retour: "m" + chouquette(0) => "m chouquette"

def chouquette(n): # Pour n = 2
    if n == 0: # Faux
        return " chouquette"
    if n > 0: # Vrai !
        return "m" + chouquette(n-1)
        # Valeur de retour: "m" + chouquette(1) => "mm chouquette"

def chouquette(n): # Pour n = 3
    if n == 0: # Faux
        return " chouquette"
    if n > 0: # Vrai !
        return "m" + chouquette(n-1)
        # Valeur de retour: "m" + chouquette(2) => "mmm chouquette"

Il est très facile de faire des erreurs qui donnent des récursions infinies en oubliant des conditions. Par exemple, le code suivant va faire une récursion infinie qui va déclencher une erreur Python:

def chouquette2(n):
    if n == 0: # initialisation
        return " chouquette"
    return "m" + chouquette2(n-1)
print(chouquette2(-1))

Traceback (most recent call last):
  File "/var/www/cha/check_py_md", line 81, in repl
    exec(code, env)
  File "<string>", line 5, in <module>
  File "<string>", line 4, in chouquette2
  File "<string>", line 4, in chouquette2
  File "<string>", line 4, in chouquette2
  [Previous line repeated 993 more times]
RecursionError: maximum recursion depth exceeded

Quand ce type d’erreurs arrivent, c’est souvent qu’un cas de base a mal été traité!

La fonction uniqueListe:

On reprend la fonction uniquelist vue dans le premier cours mais de manière récursive:

def uniquelist_rec(L):
    """  une liste contenant les éléments de $L$ sans répétition et dans l'ordre d'apparition """
    if not L: # cas de base, la liste est vide
        return []
    # Étape d'induction
    K = uniquelist_rec(L[:-1])
    if L[-1] not in K:
        K.append(L[-1])
    return K

T = [0, 2, "a", 2, "a"]
print(uniquelist_rec(T))

[0, 2, 'a']

La fonction max:

Lorsqu’on utilise la récursivité, on peut rapidement faire de petites erreurs qui ont l’air anodine mais qui ont des conséquences dramatique en terme de complexité (et de temps d’exécutions). Il faut donc faire bien attention (notamment à ne pas faire d’appels récursif multiple quand cela n’est pas nécessaire).

Par exemple,

Version récursive 1:

def recursif_max1(L):
    x = L[0]
    if len(L) == 1:
        # initialisation
        return x
    # cas général
    if x > recursif_max1(L[1:]):
        return x
    return recursif_max1(L[1:])

L = [1, 23, 2, 4, 2, 42, 17]
print(recursif_max1(L))

42

Version récursive 2:

def recursif_max2(L):
    x = L[0]
    if len(L) == 1:
        return x # initialisation
    y = recursif_max2(L[1:])
    if x > y:
        return x
    return y

print(recursif_max2(L))

42

Analyse de complexité

Bien que les deux implémentations se ressemblent, leur complexité diffère beaucoup. Pour calculer la complexité d’une fonction récursive, on doit résoudre une suite définit par récurrence. Si on note \(u_n\) la complexité de recursif_max1 et \(v_n\) la complexité de recursif_max2 alors on obtient les définitions suivantes:

\[ \begin{cases} u_0 &= 3\\ u_{n+1} &= 2u_n + 4 \end{cases} \]

et

\[ \begin{cases} v_0 &= 3\\ v_{n+1} &= v_n + 4 \end{cases} \]

Si on résoud ces suites récurrente d’ordre 1, on obtient que \(v_n=4n\) et donc la complexité de recursif_max2 est en \(O(n)\). En posant \(w_n=u_n+4\), on a que \(w_{n+1}= u_{n+1} + 4 = 2 u_n + 8 = 2(u_n + 4) = 2w_n\). Et donc \(w_n = 2^n\), ce qui donne \(u_n = 2^n - 4\) et donc une complexité pour recursif_max1 en \(O(2^n)\).

Sans surprise, la différence se voit très bien expérimentalement:

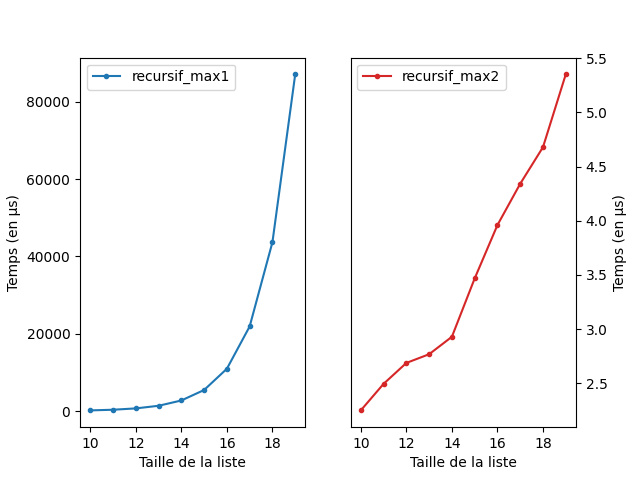
lien vers le code qui a généré l’image

itérables, itérateurs, générateurs

En Python, un objet est dit itérable s’il supporte la méthode iter qui retourne un iterateur (qu’on va voir un peu plus loin).

Par exemple:

• Les listes

L = [0, 1, "a"]
print(iter(L))

<list_iterator object at 0x7fe67c7ebf70>

• Les ensembles

S = set(L)
print(iter(S))

<set_iterator object at 0x7fe67dc80100>

• Les dictionnaires

d = {"a":"b", "c":"d"}
print(iter(d))

<dict_keyiterator object at 0x7fe67c7fcdb0>

• Les chaines de caractères

s = "reblochon"
print(iter(s))

<str_ascii_iterator object at 0x7fe67c7ebd60>

Et beaucoup d’autres.

Itérateurs

Un itérateur est itérable qui supporte l’opération de base next et dont l’opérateur iter retourne lui même.

L’opération next retourne l’élément suivant à énumérer.

Par exemple

L = ["a", 0, 1]
i = iter(L)
print(i is i)

True

print(next(i))

a

print(next(i))

0

print(next(i))

1

Quand l’itérateur est arrivé au bout, il retourne une exception:

print(next(i))

Traceback (most recent call last):
  File "/var/www/cha/check_py_md", line 81, in repl
    exec(code, env)
  File "<string>", line 1, in <module>
StopIteration

Boucle et itérateur

Pour tout élément itérable, il est possible de réaliser une boucle for e in A. La boucle for va:

• appeler iter sur l’objet A
• appeler next sur le résultat tant qu’on est pas arrivé à la fin de l’iterable.

Les itérateurs sont aussi les objets qui peuvent être utilisé par les constructeurs list et set, avec la contrainte pour ce dernier que les objets itérés soit hashable.

L = ["une", "chouquette"]
i = iter(L)
for a in i:
    print(a)

une
chouquette

for a in i:
    print(a)

Map et Reduce

Deux fonctions de fonctions très classiques sont souvent utilisées: les fonctions map et reduce. La fonction map prend en entré une fonction et un itérable et retourne un iterateur de l’image de chaque élément par la fonction.

Il est très simple de définir la fonction map en python sur les listes:

def mon_map(f, L):
    K = []
    for e in L:
        K.append(f(e))
    return K

La fonction map est également une fonction standard de Python.

Par exemple, on peut avoir la liste des carrés simplement:

def carré(x):
    return x*x

On a alors:

print(mon_map(carré, range(10)))

[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

On peut également utiliser la fonction map mais en utilisant la fonction list pour transformer l’itérateur en liste.

print(list(map(carré, range(10))))

[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

La fonction reduce permet, quant à elle, d’aplatir une liste en un objet plus simple via un parcours séquentiel. Elle prend en argument:

• une fonction de deux arguments: le premier est l’accumulateur, le deuxième un élément de la liste et retourne le nouvel état de l’accumulateur.
• une liste (un itérable en fait)
• et une valeur initiale pour l’accumulateur.

Il est très simple d’écrire le code de reduce en Python

def mon_reduce(f, L, init):
    acc = init
    for e in L:
        acc = f(acc, e)
    return acc

Comme pour map, cette fonction est présente également dans le module functools de python:

from functools import reduce

Pour faire la somme des carrés, on peut ainsi écrire:

def addition(x, y):
    return x + y

print(mon_reduce(addition, mon_map(carré, range(10)), 0))

285

Ou sans les fonctions personnalisées:

print(reduce(addition, map(carré, range(10)), 0))

285

Petit exemple avec max:

def plus_grand(x, y):
    return y if x < y else x

def fonctionnel_max(L):
    L = iter(L)
    return reduce(plus_grand, L, next(L))

print(fonctionnel_max(list(range(100))))

99

Clôture, et sous fonctions

Le mot clef def est utilisable à l’intérieur même des définitions de fonction, où il permet de définir des nouvelles fonctions localement. Cela signifie qu’on peut faire:

def g1():
    def g2():
        print("Je suis g2")
    g2()
g1()

Je suis g2

mais que la fonction g2 ne sera pas définie dans le scope:

g2()

Traceback (most recent call last):
  File "/var/www/cha/check_py_md", line 81, in repl
    exec(code, env)
  File "<string>", line 1, in <module>
NameError: name 'g2' is not defined

Ainsi, l’exemple précédant peut-être réécrit:

def fonctionnel_max2(L):
    def plus_grand(x, y):
        if x < y:
            return y
        return x
    return reduce(plus_grand, L[1:], L[0])

print(fonctionnel_max2(list(range(100))))

99

La fonction join:

En impératif, on peut coder join ainsi:

def join(L, s):
    resultat = L[0]
    for u in L[1:]:
        resultat += s + u
    return resultat

Ainsi, par exemple:

L = ["un", "millefeuille", "ça", "ne", "se refuse", "pas"]
print(join(L, ' '))

un millefeuille ça ne se refuse pas

En fonctionnel, on ferait plutôt:

def fonctionnel_join(L, s):
    def insert_s(x, y):
        return x + s + y # ici s vient du context du dessus, x et y local
    return reduce(insert_s, L, "")
print(fonctionnel_join(L, ' '))

un millefeuille ça ne se refuse pas

print(' '.join(L))

un millefeuille ça ne se refuse pas

Lambda expressions

Dans pas mal de situations, on veut écrire des fonctions rapidement, voir sur une seule ligne, juste pour les passer à map ou reduce ou autres. On peut alors utiliser pour ça les expressions lambda

Par exemple, on peut calculer la somme des carrés des 10 premiers entiers en une ligne:

print(reduce(lambda x,y:x+y, map(lambda x:x**2, range(10)), 0))

285

Les décorateurs

Il est possible de définir des fonctions de fonctions, qui sont appelées en Python, des décorateurs. La syntaxe est du Python classique:

def decore(f):
    def g():
        print("Je suis décoré !")
        return f()
    return g

patisserie2 = decore(patisserie)
res = patisserie2()
print(res)

Je suis décoré !
éclaire au chocolat

Python offre une manière de décorer les fonctions à leur définition avec la syntaxe @decorateur:

@decore
def charcuterie():
    return "Saucisson sec"
res = charcuterie()
print(res)

Je suis décoré !
Saucisson sec

Exemple de décorateur utile

Voici un décorateur bien pratique pour mesurer le temps d’exécution d’une fonction:

from time import time_ns
def temps_execution(f):
    def f_messure(*args, **kwargs):
        t1 = time_ns()
        res = f(*args, **kwargs)
        t2 = time_ns()
        print("Execution en ", (t2 - t1)/1000, "µs")
        return res
    return f_messure

On peut ainsi l’utiliser simplement:

@temps_execution
def tri(L):
    return sorted(L)

On peut ainsi facilement mesurer le temps de cette opération

from random import choices
L1 = choices(list(range(1000)), k=10**3)
tri(L1)

Execution en  125.812 µs

L2 = choices(list(range(1000)), k=10**4)
tri(L2)

Execution en  1567.879 µs

L3 = choices(list(range(1000)), k=10**5)
tri(L3)

Execution en  17013.062 µs

Compiled the: ven. 22 nov. 2024 20:25:44 CET